[알고리즘] 선분 교차 판정

 

선분 교차 판정은 CCW를 활용하여 두 선분이 교차하는지를 판단하는 테크닉이다.

 

https://baehoon.tistory.com/96

 

 

 

 

CCW를 간단히 설명하면, 세 점 A, B, C가 주어지면 벡터와 외적을 이용해 A -> B -> C로 가는 방향이 일직선인지 반시계 방향인지 시계 방향인지 세 가지 경우의 수로 나누는 알고리즘이다.

 

CCW의 반환값은 다음과 같이 도출될 수 있었다.

 

$$ CCW=(x2-x1)(y3-y1)-(y2-y1)(x3-x1) $$

\( CCW<0 \)     =>     세 점의 진행 방향이 시계 방향이다.
\( CCW>0 \)     =>     세 점의 진행 방향이 시계 방향이다.
\( CCW=0 \)     =>     세 점의 진행 방향이 시계 방향이다.

 

코드는 다음과 같다.

 

int ccw(int x1,int x2,int x3,int y1,int y2,int y3) {
		long ccw = (x2-x1)*(y3-y1) - (y2-y1)*(x3-x1);
		
		if (ccw > 0) return 1;
		else if(ccw < 0) return -1;
		else if(ccw == 0) return 0;
}

 

 

 

 

세 점의 방향성을 CCW로 알 수 있으니, 두 선분의 교차 판단도 CCW를 활용해 구할 수 있다.

 

 

두 선분이 교차한다고 말하는 것은 일반적으로 위와 같은 그림을 연상할 수 있을 것이다.

여기서 CCW를 활용 가능한데, 위 그림의 경우에서 \(\overrightarrow{ABC}\) 가 반시계, \(\overrightarrow{ABD}\) 가 시계 방향이므로, 다음과 같이 표현 가능하다.

$$ CCW(A, B, C)>0, CCW(A,B,D)<0 $$

 

즉,

 

$$ CCW(A,B,C)*CCW(A,B,D)<0 $$

 

위처럼 표현될 수 있겠다.

 

그러나 이 표현식만으로는 선분이 교차하는지를 판단할 수 없다. 다음과 같은 그림에서 반례가 발생한다.

 

 

위 그림의 경우 두 선분이 교차하지 않음에도 위 공식이 성립함을 확인할 수 있다.

이때, \(\overline{AB}\) 를 기준으로 보는 것이 아닌, \(\overline{CD}\)   를 기준으로 생각해보자.

\(\overrightarrow{CDA}\)  가 시계, \(\overrightarrow{CDB}\)  가 시계 방향이므로,

위 그림은 \(CCW(C,D,A)<0\), \(CCW(C,D,B)<0\) 이 된다.

따라서, \(\overline{CD}\) 를 기준으로 할 때도 다음과 같이 CCW 식이 되어야 한다.

$$ CCW(C,D,A)*CCW(C,D,B)<0 $$

 

그리고 이를 다시 위의 식과 함께 정리하면 선분 교차 판단의 식은 다음과 같아진다.

 

$$ CCW(A,B,C)*CCW(A,B,D)<0 \&\& CCW(C,D,A)*CCW(C,D,B)<0 $$

 

그러나 이렇게 했음에도 다음과 같은 반례가 존재한다.

 

 

\(\overrightarrow{ABC}\) 가 일직선, \(\overrightarrow{ABD}\) 가 일직선, \(\overrightarrow{CDA}\) 가 일직선, \(\overrightarrow{CDB}\) 가 일직선인 경우이다. 즉, 다음과 같은 식이 도출된다.

 

$$ CCW(A,B,C)*CCW(A,B,D)==0 \&\& CCW(C,D,A)*CCW(C,D,B)==0 $$

 

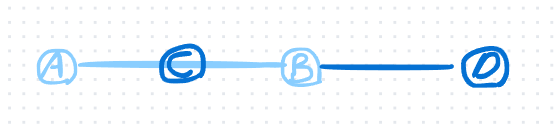
이때는 두 선분의 한 점이 한 선분 위에 포개져 있는 경우에만 선분이 교차한다고 판단해야 할 것이다.

이때까지의 조건들을 모두 정리해 코드로 작성해 보면 다음과 같다.

 

class Point {
    int x, y;

    Point(int x, int y) {
            this.x = x;
            this.y = y;
    }
}

public int ccw(Point A, Point B, Point C) {
    long ccw = (B.x-A.x)*(C.y-A.y) - (B.y-A.y)*(C.x-A.x);

    if (ccw > 0) return 1;
    else if(ccw < 0) return -1;
    else if(ccw == 0) return 0;
}

public boolean isIntersect(Point A, Point B, Point C, Point D) {
    int ccw1 = ccw(A,B,C)*ccw(A,B,D);
    int ccw2 = ccw(C,D,A)*ccw(C,D,B);

    if (ccw1 <= 0 && ccw2 <= 0) {
        if (ccw1 == 0 && ccw2 ==0) {
            // 두 선분이 일직선상에 있을 때
            // 한 점이 한 선분 위에 포개져 있는지 확인한다.
            return Math.min(A.x, B.x) <= Math.max(C.x, D.x) &&
                 Math.min(C.x, D.x) <= Math.max(A.x, B.x) &&
                 Math.min(A.y, B.y) <= Math.max(C.y, D.y) &&
                 Math.min(C.y, D.y) <= Math.max(A.y, B.y);
        }				
        return true;
    }

    return false;
}