[알고리즘] CCW(Counter-Clock-Wise)

 

 

CCW(Counter Clock Wise) 알고리즘은 세 개의 점을 이은 직선의 방향을 알고자 할 때 유용한 알고리즘이다.

기하 알고리즘의 기초라고 볼 수 있는데, 2차원 평면 위에 놓인 3개의 점이 어떤 방향성이 있는지 알려주고 이를 통해 이후 선분 교차 판정이나 볼록 껍질 등에 활용할 수 있다.

 

 

이 알고리즘은 3가지 경우의 수를 나타낸다.

1. 반시계 -> 왼쪽으로 도는지
2. 시계 -> 오른쪽으로 도는지
3. 일직선

 

CCW를 이해하기 위한 사전 지식에는 벡터와 외적이 있다.

 

벡터는 두 점을 잇는 화살표이다.

어디에서 시작해 어디로 가는지, "방향"과 "크기"를 가지고 있다.

A라는 점에서 B라는 점으로 가는 화살표가 있다면 이는 \(\overrightarrow{AB}\) 로 표현될 수 있다.

 

외적은 두 점 A,B가 있을 때, A에서 B로 회전하는 방향인 경우의 수직 벡터의 방향을 나타내는 방법이다.

3차원 좌표계에서 두 벡터의 관계를 나타내는 중요한 연산이라고 볼 수 있다.

CCW에서는 2차원 좌표의 관계를 구하는데 왜 외적이 필요한 걸까?

CCW의 오른손 법칙

 

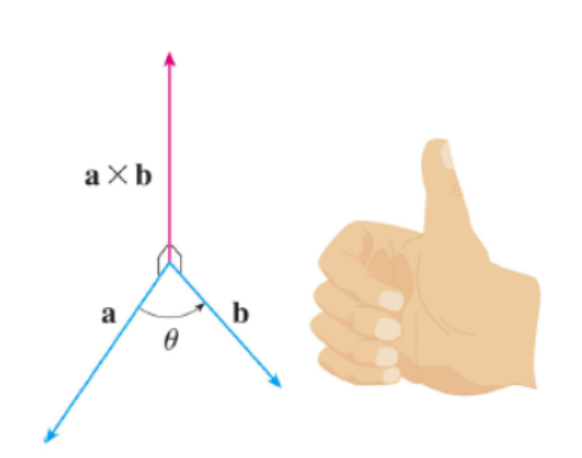
이는 이미 외적이라는 개념 자체에 ' \(\overrightarrow{A}\) 에서 \(\overrightarrow{B}\) 로 갈 때의'라는 개념이 포함되어 있기 때문이다.

이때, 위 그림의 오른손 법칙을 이해하면 편한데,

 

엄지를 제외한 손가락들을 접었을 때

• 왼쪽으로 접힌다면 수직 방향이 위(양수)가 된다 → 세 점의 방향이 반시계 방향 → 따봉
• 오른쪽으로 접힌다면 수직방향이 아래(음수)가 된다 → 세 점의 방향이 시계 방향 → 리버스 따봉

즉 A, B, C 세 점이 있을 때 \(\overrightarrow{AB}\)   , \(\overrightarrow{AC}\)  를 외적한 결괏값이 음수면 시계 방향이, 양수면 반시계 방향이, 0이면 일직선이 되는 것이 CCW 알고리즘이라고 이해할 수 있겠다.

 

 

 

결국 CCW 알고리즘을 구현하기 위해서는 두 벡터의 수직인 벡터인 \(\overrightarrow{AB}\)  , \(\overrightarrow{AC}\)  를 외적한 결괏값, 즉 3차원 좌표상의 z좌표를 구해야 하는 것을 알았다.

 

그럼 이 z 좌표를 어떻게 구해야 할까?

외적이 3차원 좌표계에서 이용되는 것이니, 3차원에서의 두 벡터에서 이를 도출해내야 한다.

 

두 벡터 \(\overrightarrow{A}\) \((a1,a2,a3) \) 와 \(\overrightarrow{B}\) \((b1,b2,b3)\)  이 있다고 하자.

두 벡터를 외적한 값은 다음과 같다.

 

이때 평면상에서의 두 벡터의 z좌표는 0이므로 a3과 b3은 0이 된다. 따라서 식은 다음과 같아진다.

 

$$ \overrightarrow{A}*\overrightarrow{B}=(0,0,a1b2-a2b1) $$

 

 

위 식에서 외적한 결괏값의 z 좌표인 \((a1*b2) - (a2*b1)\)이 바로 CCW 알고리즘의 반환값이 되는 것이다.

여기서, \(A(x1,y1)\), \(B(x2,y2)\), \(C(x3,y3)\) 세 점이 주어졌을 때 \(\overrightarrow{AB}\) 와 \(\overrightarrow{AC}\) 를 구하고 위 식에 대입하면 된다. 즉,

 

$$ \overrightarrow{AB}=(x2-x1, y2-y1), \overrightarrow{AC}=(x3-x1, y3-y1) $$

 

두 벡터를 위 \(\overrightarrow{A}\)  와 \(\overrightarrow{B}\)  에 각각 대입하면

 

$$ \overrightarrow{AB}*\overrightarrow{AC}=(0,0,(x2-x1)(y3-y1)-(y2-y1)(x3-x1)) $$

위 식처럼 나오게 된다.

 

이제 여기서 저 반환값이 0보다 크면 반시계 방향, 0보다 작으면 시계 방향, 0이라면 일직선이 된다.

식을 정리하면 다음과 같아진다.

 

\((x2-x1)(y3-y1)-(y2-y1)(x3-x1)>0\) => 반시계 방향

\((x2-x1)(y3-y1)-(y2-y1)(x3-x1)<0\) => 시계 방향

\((x2-x1)(y3-y1)-(y2-y1)(x3-x1)=0\) => 일직선

 

 

자바 코드 예시는 다음과 같다.

class Point {
    int x, y;

    Point(int x, int y) {
        this.x = x;
        this.y = y;
    }
}

int ccw(Point p1, Point p2, Point p3) {
    return (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x);
}