View
반응형
알고리즘 분류: 수학, 기하학, 많은 조건 분기
문제 링크: https://www.acmicpc.net/problem/1002
1002번: 터렛
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 $-1$ 출력한다.
www.acmicpc.net


【 풀이 】
중학교 때 배운 원의 성질을 기억하고 있다면 쉽게 해결할 수 있지만,
많은 조건을 분기해야 하므로 오답률이 꽤 높은 문제이다.
'원'이란 평면 위의 한 점에 이르는 거리가 일정한 평면 위의 점들의 집합을 의미한다.
문제에서 말하는 조규현과 백승환의 좌표는 원의 중심이라고 볼 수 있고,
류재명과의 거리는 원의 중심으로부터 류재명이 있다고 판단한 거리, 즉 반지름이 된다.
즉, 실제로 류재명이 있을 수 있는 거리는 두 원이 만나는 접점이 될 것이다.
두 원의 중심 사이의 거리를 d, 반지름의 길이를 각각 r, r` 라고 하자. (단, r < r')
두 원의 위치 관계에 따른 접점의 개수는 다음과 같다.
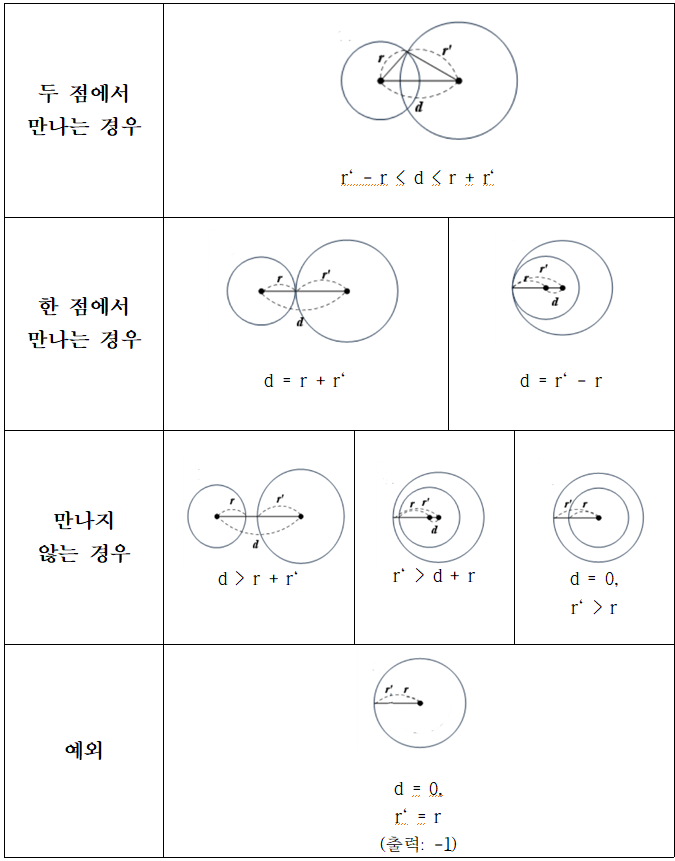
【 코드 】
#include<iostream>
#include<cmath>
using namespace std;
int main() {
int x1, y1, r1, x2, y2, r2;
int T; cin >> T;
double d;
for (int t = 0; t < T; t++) {
cin >> x1 >> y1 >> r1;
cin >> x2 >> y2 >> r2;
// 두 원의 중심 사이의 거리
d = sqrt(static_cast<double>((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)));
// 밑의 조건들은 r1 < r2 일 때의 분기이다.
// 즉 r1 > r2 일 때에는 swap으로 서로 바꿔주면 된다
if (r1 > r2)
swap(r1, r2);
if (d == 0) {
if (r1 == r2)
cout << -1 << endl;
else if (r2 > r1)
cout << 0 << endl;
}
else if (d > 0) {
if (r2 > d + r1 || d > r1 + r2)
cout << 0 << endl;
else if (d == r1 + r2 || d == r2 - r1)
cout << 1 << endl;
else if (d < r1 + r2 && r2 - r1 < d)
cout << 2 << endl;
}
}
return 0;
}
728x90
반응형
'Problem Solving > Baekjoon' 카테고리의 다른 글
| [백준] 18870번: 좌표 압축 [C++] (0) | 2023.09.21 |
|---|---|
| [백준] 1016번: 제곱 ㄴㄴ 수 [C++] (0) | 2023.09.20 |
| [백준] 10811번: 바구니 뒤집기 [C++] (0) | 2023.09.19 |
| [백준] 2667번: 단지번호붙이기 [C++] (0) | 2023.09.18 |
| [백준] 2178번: 미로 탐색 [C++] (0) | 2023.09.17 |
reply


